-
complex number 4 marks(SAQ)
Note: This section is of mathematical interest and students should be encouraged to read it. In particular, it is helpful for them to understand why the complex numbers are not really any more mathematically abstract than the reals. However, knowledge of this section is not required by the current intermediate syllabus and is not necessary for an understanding of how to use complex numbers to solve equations.
The set of complex numbers is a number system, just like the set of reals or the set of integers. Like the reals or even the integers, they were developed to close a mathematical ‘gap’ in another number system. So what is this mathematical gap?
Consider the linear equation
. This has one solution in the real numbers:
.
Now consider the equation. Algebraic manipulation shows that this is equivalent to solving
. Since squares of real numbers are non-negative we would say that this has ‘no real solutions’.
Consider finally a general quadratic equation. To solve this, we use the quadratic formula, which gives us
where
is the discriminant. If the discriminant is negative, we would again say that the equation has ‘no real solutions’.
What has happened here is that squares of real numbers are always non-negative. We cannot square a real number and get a negative number. To close this gap, we extend the reals to a number system where squares can also be negative. The easiest way to achieve this is to introduce some number whose square is
. This number
, is defined by
. Then if we want to solve
where
is some positive real, we get
, or
. If we put all numbers of the form
(where
is real) in our new number system, we can now solve any quadratic equation with real coefficients. Numbers of the form
(
real) are known as ‘imaginary numbers’.
In order to turn our set of numbers into a proper number system, we want to introduce some operations so that we can do things with these numbers. The two most fundamental operations of any set (or field) of numbers are addition (
) and multiplication (
). We will define these operations properly later. For now, all you need to know is that if you take two real numbers and add them using complex addition, the result is the same as if you added them using real addition. Similarly, if you take two real numbers and multiply them using complex multiplication, the result is the same as if you multiplied them using real multiplication.
Since the real numbers are closed under addition (
) and multiplication (
), we want this to hold true for our new number system too. What this means is that if we take any two numbers in the number system (e.g.
and
), we want their sum
to be in the number system (closure under addition).We also want their product (
) to be in the number system (closure under multiplication). If we take the closure of the real and imaginary numbers, we get all numbers of the form
(
,
real) must be in the new number system. A little bit of complex number arithmetic shows that this is enough to guarantee closure under addition and multiplication.
So now we have a new set of numbers, the complex numbers
, where each complex number
can be written in the form
(where
,
are real and
). The set of complex numbers is closed under addition and multiplication. Furthermore, each real number
is in the set of complex numbers,
, so that the real numbers are a subset of the complex numbers (see Figure 1). Finally, any quadratic equation with real coefficients, or even any polynomial with real coefficients, has solutions that can be represented as complex numbers.
Side note: Indeed what makes the complex numbers so powerful is that all degree n polynomials with complex coefficients have n (not necessarily distinct) complex roots. We say thatis ‘algebraically closed’.
Figure 1:

This figure shows that the naturals are a subset of the integers, which are a subset of the rationals, which are a subset of the reals, which are a subset of the complex numbers. The set of numbers in the reals which are not rationals are known as the irrationals.
Students should note that whilst the real numbers and the imaginary numbers are both subsets of the complex numbers, there are complex numbers (such as) which are neither real nor imaginary.
Arithmetic of Complex Numbers
Recall that every complex number is the sum of a real number and imaginary number. We say that
has a real part,
, and an imaginary part,
. If
, these are given by:
In the above notation, notice how much a complex number looks like a surd (e.g. compare
and
). The only difference is that the number under the square root sign is negative.In fact, when it comes to arithmetic, complex numbers can be treated like surds. This concept is useful when remembering how to add, subtract, multiply or divide complex numbers. Pretend that your complex number is a surd, perform the same operations and everything should work out.
Addition and Subtraction
In order to add two complex numbers, their real and imaginary parts should be added separately. In order to subtract two complex numbers, their real and imaginary parts should be subtracted separately.
Note: Addingis the same as subtracting
, and subtracting
\ is the same as adding
.
Addition: Or
Subtraction:
Or
Example 1
If the complex numbers
and
are given by
and
, determine:
a)
b)
Solution 1
a)
b)
Notice that this is just like adding or subtracting surds:
Multiplication of Complex Numbers
In order to multiply two complex numbers, each number should be treated like a surd and the FOIL method applied as appropriate. Students should note that just as the square of the irrational part of a surd gives a rational number, the square of an imaginary number gives a real number.
Example 2
If the complex numbers
and
are given by
and
, determine
.
Solution 2
(applying FOIL)
(collecting ‘like’ terms: real and imaginary parts)
Complex Conjugates and their Properties
-
-
What are Complex Numbers and why do we need them?
-
For a given complex number
, its complex conjugate is denoted by
and is given by:
Students are required to know how to determine the complex conjugate of a given complex number. The following example illustrates how this is done.
Example 3
(HSC 1994 Question 2aii)
Let, where
and
are real.Find
in the form
, where
and
are real.
Solution 3
First, express the complex number under the bar as the sum of its real and imaginary components:
To find the conjugate, replace the imaginary component with its negative counterpart
Complex conjugates have a number of nice properties:
Students will eventually be required to prove all these properties (note that proving the 4th and 6th properties requires reading ahead to the next few section). The next example illustrates how one would go about proving such results.
Example 4
For any complex numbers
and
, prove that
.
Solution 4
Let
,
Division of Complex Numbers
One nice thing about complex conjugates is that if a complex number is multiplied with its complex conjugate, the result is a real number:
Notice how this is analogous to multiplying a surd with its conjugate surd, where the result is a rational number.
This result becomes very useful when taking the reciprocals of complex numbers. Just as multiplying the top and bottom of a surd fraction by the conjugate surd of the denominator rationalises the denominator, multiplying top and bottom of a complex number fraction by the complex conjugate of the denominator makes the denominator real.
Similarly, when dividing by a complex number
, simply multiply top and bottom by the complex conjugate of
and then apply complex multiplication to the numerator.
Example 5
If the complex numbers
and
are given by
and
, determine
.
Solution 5
Equality of Complex Numbers
Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal.
if and only if
AND
Finding the Square Roots of Real and Complex Numbers
To determine the square root of a real number
:
- If
, its square roots are the real numbers
and
.
- If
,
and
are real numbers. Therefore
and
are imaginary numbers and
,
. Therefore the square roots of
are
.
Determining the square root of a complex number
is a slightly more complicated process. One way to think about it is that it is equivalent to determining which complex numbers can be squared to give
. That is, find all
real such that
. The general method is as follows:
- Use complex multiplication to obtain the real and imaginary parts of the LHS.
- Since two complex numbers are equal if and only if their real and imaginary parts are equal, equate the real and imaginary parts of the LHS and RHS to obtain two simultaneous equations:
- Comparing real parts gives
- Comparing imaginary parts gives
- Comparing real parts gives
- Solve for
and
, either by inspection or by substitution.
The following example demonstrates how both variants of the above method can be used to determine the square roots of a complex number.
Example 6
Find all complex solutions to the equation
Solution 6
Let the solutions be of the form
.
Then
so that
and
.
Variant 1:
By inspection,
,
satisfies these simultaneous equations
Checking:
and
so that
is a solution
and
so that
is a solution
Variant 2:
From the second equation,
so that
.
Substituting into the first equation yields
so that
and
or
.
Since the second equation has no real solutions,
and
.
Corresponding y can be determined using
so that
.
Therefore
and
are the solutions to the given equation.
Note that the first method, solve by inspection, is a lot shorter and tidier than the second method. Thus if students are able to determine the solutions to the two simultaneous equations by inspection, they are encouraged to use this method. Just to safe, however, they should always include a few lines of checking.
The second method has the advantage of providing a series of steps which is guaranteed to yield an answer. If a student cannot easily determine the answer by inspection they should proceed to solve the equations algebraically.
Students should note that since two simultaneous equations in two variables (
and
) yield exactly two (not necessarily distinct) solutions, each complex number has two, not necessarily distinct,complex square roots. This can be seen in Figure 2. Furthermore, as the above example illustrates, if
is a square root then
is also one. Therefore if the two complex square roots are not distinct,
and
so that
.
The conclusion is that each non-zero complex number has exactly two distinct complex square roots, and
has exactly one square root.
Using Complex Numbers to Solve Equations
Solving Quadratic Equations with Real Coefficients
Consider a general quadratic equation
.This can be solved by factorising the equation, completing the square or using the quadratic formula. The first method is usually done by inspection and so extending it to encompass complex roots would requires a degree of intuition about the behaviour of complex numbers that is beyond that which is expected from students. The second and third, however, involve algebraic manipulations that can easily be extended by using complex numbers and performing standard arithmetic calculations on complex numbers. The following example demonstrates how the roots of a quadratic equation with real coefficients can be determined using both the extended versions both of completing the square and using the quadratic formula.
Example 7
Find all complex solutions to the equation
.
Solution 7
Method 1- Completing the Square:
Starting with the equation
, completing the square yields
Method 2- Using the Quadratic Formula:
Solving Quadratic Equations with Complex Coefficients
Consider again a general quadratic equation
. This time,
,
and
are complex numbers. However, this doesn’t change the method that we use to determine the possible value of
. Solving by inspection may be a little harder, however completing the square and using the quadratic formula are still equally viable methods.
The following example illustrates how to find the roots of a quadratic equation with complex coefficients.
Example 8
Find all complex solutions to the equation
.
Solution 8
Method 1- Completing the Square:
Completing the square on the left hand side of the equation yields
so that
and
Let
,
,
real.
Notice how in this step, we don’t automatically jump to ‘let
’. This is because we know that the quantities that we’re most familiar with dealing with the real and imaginary parts of the number being squared. Of course, it is also fine to let
, but the working will probably be a little more tedious and a little less familiar.
Then
so that
and
.
The first equation gives
The second equation gives
so that
and
.
or
or
Method 2- Using the Quadratic Formula:
Here the square roots of
need to be obtained. This can be done using the same method as the one used above, where all pairs of
and
satisfying
are determined. This leads to solving the simultaneous equations
and
.
The solutions to the simultaneous equations can be attained by inspection or through algebraic manipulation and yield
.
or
or
The Argand Diagram
For every real
and
there exists a complex number given by
. From before, if the real parts and the imaginary parts of two complex numbers are equal, then they are the same number. This means that for every real
and
there exists a unique complex number given by
. In other words, there is a 1-1 correspondence between ordered pairs of reals
and the complex numbers. Extending the idea a little further, there is a 1-1 correspondence between the complex numbers and the points in the x-y plane.
This correspondence immediately suggests a way to diagrammatically represent a complex number
: on the x-y plane, with x and y coordinates corresponding to
and
respectively. Such a diagram is known as an ‘Argand diagram’ and the plane on which the points are plotted is sometimes referred to as the ‘Argand plane’ or the ‘complex plane’. The x-axis, along which the value of
can be determined, is referred to as the ‘real axis’ and the y-axis is referred to as the ‘imaginary axis’.
The following example demonstrates how to represent complex numbers of the form
on an Argand diagram.
Example 9
and
- If
If is restricted by
, the value of
is unique. If not, there is an infinite family of solutions given by adding
(
an integer) to the value of
between
and
.
Note that if (i.e.
),
and all values of
are possible.
For a compvvWhat are Complex Numbers and why do we need them?
Note: This section is of mathematical interest and students should be encouraged to read it. In particular, it is helpful for them to understand why the complex numbers are not really any more mathematically abstract than the reals. However, knowledge of this section is not required by the current HSC syllabus and is not necessary for an understanding of how to use complex numbers to solve equations.
The set of complex numbers is a number system, just like the set of reals or the set of integers. Like the reals or even the integers, they were developed to close a mathematical ‘gap’ in another number system. So what is this mathematical gap?
Consider the linear equation . This has one solution in the real numbers:
.
Now consider the equation . Algebraic manipulation shows that this is equivalent to solving
. Since squares of real numbers are non-negative we would say that this has ‘no real solutions’.
Consider finally a general quadratic equation . To solve this, we use the quadratic formula, which gives us
where
is the discriminant. If the discriminant is negative, we would again say that the equation has ‘no real solutions’.
What has happened here is that squares of real numbers are always non-negative. We cannot square a real number and get a negative number. To close this gap, we extend the reals to a number system where squares can also be negative. The easiest way to achieve this is to introduce some number whose square is . This number
, is defined by
. Then if we want to solve
where
is some positive real, we get
, or
. If we put all numbers of the form
(where
is real) in our new number system, we can now solve any quadratic equation with real coefficients. Numbers of the form
(
real) are known as ‘imaginary numbers’.
In order to turn our set of numbers into a proper number system, we want to introduce some operations so that we can do things with these numbers. The two most fundamental operations of any set (or field) of numbers are addition () and multiplication (
). We will define these operations properly later. For now, all you need to know is that if you take two real numbers and add them using complex addition, the result is the same as if you added them using real addition. Similarly, if you take two real numbers and multiply them using complex multiplication, the result is the same as if you multiplied them using real multiplication.
Since the real numbers are closed under addition () and multiplication (
), we want this to hold true for our new number system too. What this means is that if we take any two numbers in the number system (e.g.
and
), we want their sum
to be in the number system (closure under addition).We also want their product (
) to be in the number system (closure under multiplication). If we take the closure of the real and imaginary numbers, we get all numbers of the form
(
,
real) must be in the new number system. A little bit of complex number arithmetic shows that this is enough to guarantee closure under addition and multiplication.
So now we have a new set of numbers, the complex numbers , where each complex number
can be written in the form
(where
,
are real and
). The set of complex numbers is closed under addition and multiplication. Furthermore, each real number
is in the set of complex numbers,
, so that the real numbers are a subset of the complex numbers (see Figure 1). Finally, any quadratic equation with real coefficients, or even any polynomial with real coefficients, has solutions that can be represented as complex numbers.
Side note: Indeed what makes the complex numbers so powerful is that all degree n polynomials with complex coefficients have n (not necessarily distinct) complex roots. We say that is ‘algebraically closed’.
Figure 1:
 |
This figure shows that the naturals are a subset of the integers, which are a subset of the rationals, which are a subset of the reals, which are a subset of the complex numbers. The set of numbers in the reals which are not rationals are known as the irrationals.
Students should note that whilst the real numbers and the imaginary numbers are both subsets of the complex numbers, there are complex numbers (such as ) which are neither real nor imaginary.
Arithmetic of Complex Numbers
Recall that every complex number is the sum of a real number and imaginary number. We say that has a real part,
, and an imaginary part,
. If
, these are given by:
|
|
In the above notation, notice how much a complex number looks like a surd (e.g. compare and
). The only difference is that the number under the square root sign is negative.In fact, when it comes to arithmetic, complex numbers can be treated like surds. This concept is useful when remembering how to add, subtract, multiply or divide complex numbers. Pretend that your complex number is a surd, perform the same operations and everything should work out.
Addition and Subtraction
In order to add two complex numbers, their real and imaginary parts should be added separately. In order to subtract two complex numbers, their real and imaginary parts should be subtracted separately.
Note: Adding is the same as subtracting
, and subtracting
\ is the same as adding
.
| Addition: Or Subtraction: Or |
Example 1If the complex numbers a) b) Solution 1a)
|
Notice that this is just like adding or subtracting surds:
Multiplication of Complex Numbers
In order to multiply two complex numbers, each number should be treated like a surd and the FOIL method applied as appropriate. Students should note that just as the square of the irrational part of a surd gives a rational number, the square of an imaginary number gives a real number.
| |
Example 2If the complex numbers Solution 2
|
Complex Conjugates and their Properties
For a given complex number , its complex conjugate is denoted by
and is given by:
| |
Students are required to know how to determine the complex conjugate of a given complex number. The following example illustrates how this is done.
Example 3(HSC 1994 Question 2aii) Solution 3First, express the complex number under the bar as the sum of its real and imaginary components: |
Complex conjugates have a number of nice properties:
| |
Students will eventually be required to prove all these properties (note that proving the 4th and 6th properties requires reading ahead to the next few section). The next example illustrates how one would go about proving such results.
Example 4For any complex numbers Solution 4Let
|
Division of Complex Numbers
One nice thing about complex conjugates is that if a complex number is multiplied with its complex conjugate, the result is a real number:
| |
Notice how this is analogous to multiplying a surd with its conjugate surd, where the result is a rational number.
This result becomes very useful when taking the reciprocals of complex numbers. Just as multiplying the top and bottom of a surd fraction by the conjugate surd of the denominator rationalises the denominator, multiplying top and bottom of a complex number fraction by the complex conjugate of the denominator makes the denominator real.
Similarly, when dividing by a complex number , simply multiply top and bottom by the complex conjugate of
and then apply complex multiplication to the numerator.
Example 5If the complex numbers Solution 5
|
Equality of Complex Numbers
Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal.
if and only if
|
Finding the Square Roots of Real and Complex Numbers
To determine the square root of a real number :
- If
, its square roots are the real numbers
and
.
- If
,
and
are real numbers. Therefore
and
are imaginary numbers and
,
. Therefore the square roots of
are
.
Determining the square root of a complex number is a slightly more complicated process. One way to think about it is that it is equivalent to determining which complex numbers can be squared to give
. That is, find all
real such that
. The general method is as follows:
- Use complex multiplication to obtain the real and imaginary parts of the LHS.
- Since two complex numbers are equal if and only if their real and imaginary parts are equal, equate the real and imaginary parts of the LHS and RHS to obtain two simultaneous equations:
- Comparing real parts gives
- Comparing imaginary parts gives
- Comparing real parts gives
- Solve for
and
, either by inspection or by substitution.
The following example demonstrates how both variants of the above method can be used to determine the square roots of a complex number.
Example 6Find all complex solutions to the equation Solution 6Let the solutions be of the form Then so that Variant 1: By inspection, Checking:
Variant 2: From the second equation, Substituting into the first equation yields so that Since the second equation has no real solutions, Corresponding y can be determined using Therefore Note that the first method, solve by inspection, is a lot shorter and tidier than the second method. Thus if students are able to determine the solutions to the two simultaneous equations by inspection, they are encouraged to use this method. Just to safe, however, they should always include a few lines of checking. The second method has the advantage of providing a series of steps which is guaranteed to yield an answer. If a student cannot easily determine the answer by inspection they should proceed to solve the equations algebraically. |
Students should note that since two simultaneous equations in two variables ( and
) yield exactly two (not necessarily distinct) solutions, each complex number has two, not necessarily distinct,complex square roots. This can be seen in Figure 2. Furthermore, as the above example illustrates, if
is a square root then
is also one. Therefore if the two complex square roots are not distinct,
and
so that
.
The conclusion is that each non-zero complex number has exactly two distinct complex square roots, and has exactly one square root.
Using Complex Numbers to Solve Equations
Solving Quadratic Equations with Real Coefficients
Consider a general quadratic equation .This can be solved by factorising the equation, completing the square or using the quadratic formula. The first method is usually done by inspection and so extending it to encompass complex roots would requires a degree of intuition about the behaviour of complex numbers that is beyond that which is expected from students. The second and third, however, involve algebraic manipulations that can easily be extended by using complex numbers and performing standard arithmetic calculations on complex numbers. The following example demonstrates how the roots of a quadratic equation with real coefficients can be determined using both the extended versions both of completing the square and using the quadratic formula.
Example 7Find all complex solutions to the equation Solution 7Method 1- Completing the Square: Starting with the equation
|
Solving Quadratic Equations with Complex Coefficients
Consider again a general quadratic equation . This time,
,
and
are complex numbers. However, this doesn’t change the method that we use to determine the possible value of
. Solving by inspection may be a little harder, however completing the square and using the quadratic formula are still equally viable methods.
The following example illustrates how to find the roots of a quadratic equation with complex coefficients.
Example 8Find all complex solutions to the equation Solution 8Method 1- Completing the Square: Completing the square on the left hand side of the equation yields
so that Let Notice how in this step, we don’t automatically jump to ‘let Then The first equation gives The second equation gives
Method 2- Using the Quadratic Formula:
Here the square roots of The solutions to the simultaneous equations can be attained by inspection or through algebraic manipulation and yield
|
The Argand Diagram
For every real and
there exists a complex number given by
. From before, if the real parts and the imaginary parts of two complex numbers are equal, then they are the same number. This means that for every real
and
there exists a unique complex number given by
. In other words, there is a 1-1 correspondence between ordered pairs of reals
and the complex numbers. Extending the idea a little further, there is a 1-1 correspondence between the complex numbers and the points in the x-y plane.
| |
This correspondence immediately suggests a way to diagrammatically represent a complex number : on the x-y plane, with x and y coordinates corresponding to
and
respectively. Such a diagram is known as an ‘Argand diagram’ and the plane on which the points are plotted is sometimes referred to as the ‘Argand plane’ or the ‘complex plane’. The x-axis, along which the value of
can be determined, is referred to as the ‘real axis’ and the y-axis is referred to as the ‘imaginary axis’.
The following example demonstrates how to represent complex numbers of the form on an Argand diagram.
Example 9 |
lex number , the corresponding values of
and
are given special names.
- The quantity
is called the modulus of
and is denoted by |z|.
- All possible values of
are called arguments of
and are denoted by
. The unique value of
that is between
and
is known as the principal argument of
and is denoted by
.
- Note: The capitalised A is very important: it differentiates the principal argument from other arguments.
- If
is not the principal argument then it is incorrect to write
.
- If
it is still correct to write
, but some information is lost in doing so.
- If
- Note also that the complex number 0 does not have a defined principal argument. By convention, 0 does not have an argument.
| Modulus: Arguments: where Principal Argument: where |
Just as two complex numbers are equal if and only if their real and imaginary parts are both equal, two complex numbers are equal if and only if their moduli and principal arguments are equal. (The obvious exception is the complex number 0, which does not have a defined principal argument.)
The modulus of a complex number of the form is easily determined. Students tend to struggle more with determining a correct value for the argument. One method is to find the principal argument using a diagram and some trigonometry. The following example illustrates how this can be done.
Example 10For the complex number Solution 10
Let Most students would solve the trigonometric equation by plugging |
From the relationships between ,
,
and
, it can be determined that a complex number
can also be written in the form
or
, where
is standard shorthand notation for
. This is known as the ‘modulus-argument form’, or ‘mod-arg form’ of a complex number.
| Mod – Arg Form: |
The next example demonstrates the process in a typical conversion between Cartesian form and mod-arg form, and illustrates how to decide on a form to use.
Example 11Let i. Express ii. Express Solution 11i.
|
Multiplication and Division of Complex Numbers and Properties of the Modulus and Argument
Students should ensure that they are familiar with how to transform between the Cartesian form and the mod-arg form of a complex number. This is because questions involving complex numbers are often much simpler to solve using one form than the other form. In particular, when complex numbers are multiplied or divided, their moduli and arguments have much simpler and cleaner relationships than their real and imaginary components. This means that in questions involving multiplication and division of complex numbers, it is often recommended to convert to modulus-argument form and complete the calculation before converting back (if conversion is necessary).
The relationships that students are required to know how to derive are:
| Properties of the Modulus: |
Properties of the Argument:
|
Students should be able to prove all of these relations. The following example illustrates how to prove the first property in each box.
Example 12Let a) Express b) Hence show that Solution 12a)
|
The proof for the second property is similar to that of the first. For positive integers the third property can be derived using the first property and mathematical induction. For negative integers
the third property can be derived using
and the second property. These proofs are left as an exercise to the reader.
The following worked examples illustrate how the above properties can be used in calculations in mod-arg form.
Example 13Given i. Find the argument and modulus of ii. Find the smallest positive integer Solution 13i.
If |
Example 14 (HSC 1997 Q2d)Let i. Find ii. Hence find two distinct ways of writing Solution 14i.
We note two interesting things given in the question: we want to find By the properties of the modulus, Similarly |
Example 15i. If ii. Solution 15i. We wish to prove that
|
Geometric Relationships between points on an Argand Diagram
There are nice geometrical relationships between points representing certain complex numbers. In particular, students are required to recognise the relationship between the point representing a complex number and the points representing the complex numbers
,
(
real) and
. These can be summarised as follows:
| |
Students are not required to know the proofs of these properties. However, the proofs have been included as they help to illustrate some basic principles used in graphing complex numbers and relationships between complex numbers.
Relationship between Points Representing 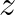 and
and 
If is represented by the point
then
is represented by the point
. This is the reflection of
over the x-axis.
Similarly, if is represented by the point
then
and is represented by the point
, which is again obviously the reflection of
over the x-axis.

Relationship between Points Representing 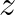 and
and 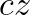 (
( is real)
is real)
If is represented by the point
then
is represented by the point
.
Similarly, if is represented by the point
then
is represented by the point
.
This means that the vector is the dilation of the vector
about the origin with factor
.
That is:
- If
, stretch out
by a factor of
- If
, stretch out
by a factor of
and rotate it by
about the origin
- If
then the point representing
is the point

Relationship between Points Representing 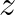 and
and 
If is represented by the point
then
is represented by the point
. This means that the vector
is the vector
rotated anticlockwise
radians, or
, about the origin, since its magnitude is the same but its angle of rotation is
radians larger.

Note that in this case, since the calculations involve multiplying complex numbers, it is a lot simpler to use mode-arg form. If were instead represented in Cartesian form, then
represented by the point
and
is represented by the point
.The relationship between these points is not as immediately obvious.
The following example demonstrates how the relationships between the points representing ,
,
(
real) and
can be used to determine the complex numbers represented by certain points in terms of the complex numbers represented by other points.
Example 16(i) Let (ii) The square is now rotated about Solution 16a) A good approach to an Argand diagram question always begins with a diagram. Diagrams help you to see properties or make links that you otherwise would have missed. b) Again, start with a diagram
|
Representing Complex Numbers as Vectors on an Argand Diagram
We showed before that there is a 1-1 correspondence between the complex numbers and the points in the x-y plane, so that each complex number can be represented by a unique point in the complex plane. This means that there is also a 1-1 correspondence between the complex numbers and the vectors
, where
is the origin and
is a point in the complex plane.
We represent each complex number by the vector
, where
. From the definition of the modulus and argument, we see that this means that:
- The length of the vector
is the distance from
to the origin, which is the modulus
i.e. - The direction of the vector
is defined by the angle from the positive x axis to the ray
, which is the argument. This means that the direction of the vector
is uniquely defined by
.
So we see that this vector representation is similar to the Argand diagram representation. What this representation adds to the point representation is that vectors can be moved about, whereas points are fixed in the plane. Figure 3 illustrates this concept. This means that a lot of geometric properties (and hence algebraic properties) can be determined by rearranging the vectors.
 Figure 3 Figure 3 |
Although vectors |
Constructing Vector Representations of Complex Numbers
Given the vector representations of two complex numbers and
, students are required to construct the vectors
,
,
and
. This can be done by considering the geometrical properties of the vectors.
Two vectors, and
, can be added either by using the triangle method or by using the parallelogram method. Each method is equally viable and in different situations one method will be more useful than the other.
The triangle method, or the tip-to-tail method, involves placing the tip of the vector at the tail of the vector
. The vector pointing from the remaining tail to the remaining tip, i.e. from the tail of
to the tip of
, gives the vector
.
The parallelogram method involves placing the tails of each vector at the same spot. If the parallelogram with and
as two of its adjacent sides is constructed, the vector along the diagonal from the tails to the opposite vertex gives the vector
.

Note that the vector is the vector with the same magnitude as
but in the opposite direction.
Note also that subtracting a vector is the same as adding the vector
.
Constructing the Point Representing  from the Points Representing
from the Points Representing 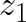 and
and 
Given the points representing and
, the vectors representing
and
with tail at the origin can be obtained by joining the points with the origin. Since the vectors representing
and
are placed tail to tail, the parallelogram method can then be used to construct the vector representing
with tail at the origin. The tip of this vector gives the point representing
.
Students must include:·
|
 |
Constructing Vectors Representing  and
and  from Vectors Representing
from Vectors Representing 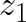 and
and 
Given the vectors and
representing
and
respectively, vectors representing
and
with tip at the origin are given by
and
respectively. Since
and
are placed tip to tail, the triangle method can then be used to construct a vector representing
by adding
and
. The same method holds for constructing a vector representing
.
Students must include:·
|
 |
 |
Constructing the Point Representing  from the Points Representing
from the Points Representing 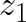 and
and 
Suppose the points representing and
are given by
and
. Denote by
the point
. Use equal angles to construct the similar triangles
and
. Then
is the point representing
.
Students must include:
|
 |
To see why this is true, consider and the angle from the positive x axis to the ray
,
.
By similar triangles, so that
.
Again by similar triangles,
so that .
Together, these tell us that is the point representing
.
Triangle Inequality
Students are expected to be able to prove the triangle inequality for the moduli of complex numbers:
| |
The geometrical proof of this given in the following worked example and demonstrates one application of vector representations.
Example 17Given two arbitrary complex numbers Solution 17
|
Worked Examples involving Vector Representations of Complex Numbers
HSC questions do not simply ask students to draw a memorised diagram. Students are often required to synthesise the information embedded in the above techniques, such as by identifying the third side of the triangle ,
as the vector
, or even using algebra to determine other geometric properties. The following examples illustrate a few applications of the techniques presented in this section.
Example 18Let (i) On an Argand diagram plot the points (ii) Plot the points Solution 18Graphs for (i) and (ii):
(i) Since (ii) By the triangle rule for vector subtraction the vector |
Example 19
Solution 19(i) The proof follows the same lines as the proof for (ii) The point
We guess that the previous parts of the question should help us to answer this question. |
Example 20In an Argand Diagram,
|
De Moivre’s Theorem
De Moivre’s Theorem states that for all integers :
| |
This result is equivalent to .
The result is trivial for and can be proven for positive integers
by mathematical induction, using the expansions of
and
. It can then be extended to the negative integers using complex division and
. The proof is left as an exercise to the reader.
The most obvious application of De Moivre’s theorem is in calculating integer powers of complex numbers. For any complex number , De Moivre’s theorem tells us that
. This means that integer powers of a complex number can be easily calculated using De Moivre’s theorem and the modulus-argument form of the number. The following example illustrates how to calculate the integer power of a complex number.
Example 21Express in modulus-argument form: (i) (ii) Solution 21(i)
|
De Moivre’s theorem is actually a lot more powerful than it looks. As was just demonstrated, directly comparing the two sides of the equation provides a direct formula for powers of complex numbers. However, the real and imaginary components can also be compared separately. Doing so provides an efficient way of calculating and
as polynomials in
and
. The following example illustrates how this is done.
Example 22se De Moivre’s thorem to express Solution 22Since we want to express
|
De Moivre’s theorem is also useful because it provides an efficient way of expressing large powers of and
as a linear combination of the sines and cosines of multiples of
. This is because if we let
:
The next example demonstrates how De Moivre’s theorem can be used to calculate large powers of and
.
Example 23If Solution 23Let Then
From this, we know that
|
The  Roots of Unity
Roots of Unity
The nth roots of unity are the complex numbers such that
. These can be determined using de Moivre’s theorem:
Let . Then
. Since two non-zero complex numbers can only be equal if their moduli are equal,
so that
. This gives
,
and
,
. This yields
distinct values for
corresponding to
. Any other value of
yields a value of
that gives the same sine and cosine values as one of the n values of
specified above.
Therefore the n nth roots of unity are given by .
This shows that nth roots of unity can be expressed on the Argand diagram as vectors of length 1 radiating from the origin, spaced equally around the unit circle. This means that they form the vertices of a regular n-gon. Students will often be asked to demonstrate their understanding of this through graphing the nth roots on an Argand diagram. For example, the cube roots of unity can be represented as the vertices of an equilateral triangle as follows:
Students must include:
|
 |
The roots can be found in the form by converting from modulus-argument form.
The nth roots of can similarly be determined using de Moivre’s theorem:
Let . Then
.
,
and
and
,
.
Where |
Again, the roots must be equally spaced around the unit circle. However, they look a little different to the nth roots of unity. One way to think about it is that whereas nth roots of unity begin at 1 and move around the circle anticlockwise with a step angle of , nth roots of unity begin at -1 and move around the circle anticlockwise with a step angle of
. Another way to think about it is that each nth root of -1 is of the form
, which is one of the nth roots of unity rotated anticlockwise about the origin by an angle of
.
Polynomials and the  Roots of
Roots of 
One of the more difficult applications of complex number theory involves using the algebra and ideas expressed in de Moivre’s theorem and the derivation of expression for the nth roots of to solve polynomials. These questions can usually be broken down into little steps by using complex number theory and ideas involved in solving polynomials, such as sum and product of roots. The nice thing is that HSC questions will often help students to separate the question into simple steps, or even present the steps and links as part of the problem statement. However, since this is not always the case, students should acquaint themselves with the various processes involved in breaking down questions.
Often, smaller steps can be obtained by considering the type of information given to them in the problem statement and the type of information that they needs to be extract. The following examples illustrate how this can be done.
Example 24
showing that the nth roots of unity can be written as powers of one of its roots, dividing through by
|
This problem demonstrates a type of problem that many students will shy away from: one involving not 1, not 2, but n variables. The trick is to deal with each variable separately, or to work patiently through sums, preferably using summation notation. Students will see that this question, as scary as it looks, is actually a lot easier than the previous one.Let the points (i) Prove that (ii) Show that (iii) Prove that Solution 25(i) We want to know the value of
(iii) Before we dive into summation, let’s see if we can simplify each term in the expression any more.
|
Sketching Curves and Regions in the Complex Plane
Sometimes it is useful to represent the complex solutions to a given equation or inequality in graphical form. In particular, there are a few standard curves that students are expected to know how to sketch. In the HSC, the complex equations describing these curves are often combined or turned into inequalities to create more involved questions. However, these curves and regions are quite simple to sketch if students have a firm understanding of the elementary curves that they are comprised of.
When determining the nature of the following standard curves, a number of algebraic and geometric approaches can be taken.If using an algebraic approach, students should ensure that they are able to obtain a Cartesian equation for the locus, and able to translate this equation into a geometric description.If using the geometric approach, students should ensure that they are able to translate the geometric properties describing the locus into algebraic form, through a Cartesian equation.
Solutions to the Equations  and
and 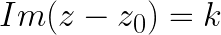
Algebraic approach
The solutions of these equations are given by lines parallel to the y axis and x axis respectively:
If ,
.If
.
 |
 |
Solutions to Equations of the Form 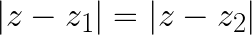
Algebraic approach
Since the equations involve the subtraction of complex numbers,the simpler algebraic approach should involve expressing the complex numbers as the sum of their real and imaginary parts.
Let ,
and
.
which is of the form
, a straight line!
Geometric approach
This seems like a remarkably simple result for some not-so-simple equations. However it is quite easily explained using a geometric interpretation. The solutions describe the locus of points that are equidistant from two fixed points in the plane: the point representing
and the point
representing
. If a possible value of
is represented by the point
, then
is isosceles with
so that the altitude from
to
bisects
. That is,
lies on the perpendicular bisector of
, which is a straight line. Furthermore, any point on the perpendicular bisector satisfies
so that the locus of points is the perpendicular bisector.
To plot the perpendicular bisector of , all that is required is to find a point on the line and the gradient of the line.
A point on the line is given by the midpoint of . The gradient is the one perpendicular to the gradient of
.
These give .
Students must include:
|
 |
Solutions to Equations of the Form 
Algebraic approach
Again, since the equations involve the subtraction of complex numbers, the simpler algebraic approach should involve expressing the complex numbers as the sum of their real and imaginary parts.
Let and
.
The locus of therefore traces out a circle in the complex plane center
and radius
.
Geometric approach
The solutions describe the locus of points that are a fixed distance from the point representing the complex number
. Thus the locus of
traces out a circle in the complex plane center
and radius
. This has equation
.
Students must include:
|
 |
Solutions to Equations of the Form 
The graph is a ray starting with an open circle on the point representing the complex number
and pointing in a direction that is
anticlockwise from the positive x-axis.
Students must include:
|
 |
Geometric approach
Consider the vector representation of complex numbers, where is the angle from the positive x-axis to the ray
. Since
is the vector pointing from the point
representing
to the point
representing
, if this makes an angle of
with the positive x-axis then the ray
is
radians anticlockwise from the positive x-axis. Similarly if
is represented by an arbitrary point
on the ray with tail
and angle
from positive x-axis, then
as required. At
or
is undefined so that there is an open circle at that point.
Equations involving both 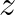 and
and 
Students will often be asked to graph equations involving both and
. Cartesian equations can usually be obtained by substituting
and
.
Worked Examples involving Sketching Curves and Regions in the Complex Plane
Sketching the solutions to inequalities is not any more difficult than sketching the solutions to equalities. The equality case creates a curve, or boundary, that splits the complex plane into two sections. The inequality sign means that everything on one side of the boundary is part of the region and everything on the other side is not.
The following examples illustrate how compositions of elementary curves can be used to graph regions in the complex plane that are described by a number of equations and inequalities.
Example 26Sketch the region where the inequalities Solution 26The trick with sketching composite regions is to sketch each region separately, and see which parts of the plane lie in both regions.
Taking the intersection of these two regions yields:
|
Example 27On an Argand diagram, shade in the region determined by the inequalities Solution 27
|











 describes the set of points equidistant from the points
describes the set of points equidistant from the points 

 Note the open circle at
Note the open circle at 
You must be logged in to post a comment.